Probability Density Function nde-ed.org The ability to understand and apply Business Statistics is becoming increasingly important in the industry. A good understanding of Business Statistics is a requirement to make correct and relevant interpretations of data.
Econometrics and the Probability Density Function (PDF
Probability Density Function Definition. A probability density function (PDF) shows the probabilities of a random variable for all its possible values. The probabilities associated with specific values …, Probability Density Function (pdf) If a random variable X takes on infinite number of possible values in the interval on a real line, then the variable is known as continuous random variable. Consider the random variable X to be continuous then the function f ( x ) and for any two numbers a and b such that a £ b , is called probability density function if the following are true..
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function that describes the relative likelihood for this random variable to take on a … A discrete probability distribution function (PDF) has two characteristics: Each probability is between zero and one, inclusive. The sum of the probabilities is one. Example 4.1. A child psychologist is interested in the number of times a newborn baby's crying wakes its mother after midnight. For a random sample of 50 mothers, the following information was obtained. Let X = the number of times
Probability function is used to refer to either probability mass function(the probability function of discrete random variable) or probability density function(the probability function of continuous random variable). Probability Distribution Function (PDF) a mathematical description of a discrete random variable ( RV ), given either in the form of an equation (formula) or in the form of a table listing all the possible outcomes of an experiment and the probability associated with each outcome.
The probability distribution of a continuous random variable is represented by an equation, called the probability density function (pdf). All probability density functions satisfy the following conditions: In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function that describes the relative likelihood for this random variable to take on a …
The binomial distribution gives the probability of observing exactly k successes. The dbinom function in R will comput e this probability for you: dbinom(k, n, p) Note that the binomial distribution is a discrete distribution. That is, it only makes sense for integer values of k. You can’t ask : what is the probab ility of observing 4.3 heads in ten coin tosses. Also note that the binomial Probability density function and the cumulative distribution function are known to be functions that are quite different when it comes to calculating statistics. Here are the notable differences between the two based on how they actually work.
The probability distribution function / probability function has ambiguous definition. They may be referred to: They may be referred to: Probability density function (PDF) A probability density function (pdf) is a way of describing the data that has been collected from a measurement or multiple measurements. Probability density is simply the probability of a variable existing between two values that bound an interval.
Probability Distribution Function (PDF) a mathematical description of a discrete random variable ( RV ), given either in the form of an equation (formula) or in the form of a table listing all the possible outcomes of an experiment and the probability associated with each outcome. Sometimes, it is referred to as a density function, a PDF, or a pdf. For a continuous probability distribution, the density function has the following properties: Since the continuous random variable is defined over a continuous range of values (called the domain of the variable), the graph of the density function will also be continuous over that range. The area bounded by the curve of the
Sometimes, it is referred to as a density function, a PDF, or a pdf. For a continuous probability distribution, the density function has the following properties: Since the continuous random variable is defined over a continuous range of values (called the domain of the variable), the graph of the density function will also be continuous over that range. The area bounded by the curve of the Discrete Probability Density Function The discrete probability density function (PDF) of a discrete random variable X can be represented in a table, graph, or formula, and provides the probabilities Pr(X = x) for all possible values of x.
Probability density function (PDF), in statistics, a function whose integral is calculated to find probabilities associated with a continuous random variable (see continuity; probability theory). Its graph is a curve above the horizontal axis that defines a total area, between itself and the axis, of 1. The percentage of this area included between any two values coincides with the probability In probability and statistics, it is the function that describe the probability distribution of the possible values of a random variable. Learn more in: OLAP over Uncertain and Imprecise Data Streams
The Cumulative Distribution Function for a Random Variable \ Each continuous random variable has an associated \ probability density function (pdf) 18/08/2018В В· As Probability density function is the derivative of Cumulative distribution function, therefore Cumulative distribution function (CDF) is also explained before describing the probability density
1 Probability Distributions Consider a continuous, random variable (rv) Xwith support over the domain X. The probability density function (PDF) of Xis the function f X(x) such that for any two numbers aand bin the domain X, with a 4.1 Probability Distribution Function (PDF) for a. The probability distribution function / probability function has ambiguous definition. They may be referred to: They may be referred to: Probability density function (PDF), Definition of Probability Density Function (PDF): The probability that values between x and x + dx are found with probability p(x). Receive a 20% Discount on All Purchases Directly Through IGI Global's Online Bookstore.. Probability Density Function nde-ed.org. I understand that the probability density function, pdf, of a continuous random variable is the probability of the variable taking on a given value. I also thought that for a continuous random variable, the probability of it taking a specific value is always 0 i.e. P(X=x) = 0., The probability distribution of Example 3.9, for example, also applies to the random variable Y, where Y is the number of heads when a coin is tossed 4 times, or to the random variable W, where W is the number of red cards that occur when. 3.1 Concept of a Random Variable University of Minnesota. A probability density function (pdf) is a way of describing the data that has been collected from a measurement or multiple measurements. Probability density is simply the probability of a variable existing between two values that bound an interval. A probability density function captures the probability of being close to a number even when the probability of any single number is zero.. The TI 83 normalPDF function, accessible from the DISTR menu will calculate the normal probability density function, given the mean μ and standard deviation σ. The function doesn’t actually give you a probability, because the normal distribution curve is continuous. Probability density function (PDF), in statistics, a function whose integral is calculated to find probabilities associated with a continuous random variable (see continuity; probability theory). Its graph is a curve above the horizontal axis that defines a total area, between itself and the axis, of 1. The percentage of this area included between any two values coincides with the probability I understand that the probability density function, pdf, of a continuous random variable is the probability of the variable taking on a given value. I also thought that for a continuous random variable, the probability of it taking a specific value is always 0 i.e. P(X=x) = 0. Arguably the single most important PDF is the Normal (a.k.a., Gaussian) probability distribution function (PDF). Among the reasons for its popularity are that it is theoretically elegant, and arises In the example, a probability density function and a transformation function were given and the requirement was to determine what new probability density function results. Suppose instead that two probability density functions are given and the requirement is The distribution of a continuous random variable can be characterized through its probability density function (pdf). The probability that a continuous random variable takes a value in a given interval is equal to the integral of its probability density function over that interval, which in turn is equal to the area of the region in the xy-plane bounded by the x-axis, the pdf and the vertical Joint Probability Density Function If you have continuous variables , they can be described with a probability density function (PDF) . Unlike the discrete variable example above, you can’t write out every combination of every variable because you would have infinite possibilities to write out (which is, of course, impossible). Probability density function and the cumulative distribution function are known to be functions that are quite different when it comes to calculating statistics. Here are the notable differences between the two based on how they actually work. Joint Probability Density Function If you have continuous variables , they can be described with a probability density function (PDF) . Unlike the discrete variable example above, you can’t write out every combination of every variable because you would have infinite possibilities to write out (which is, of course, impossible). In probability and statistics, it is the function that describe the probability distribution of the possible values of a random variable. Learn more in: OLAP over Uncertain and Imprecise Data Streams 1 Probability Distributions Consider a continuous, random variable (rv) Xwith support over the domain X. The probability density function (PDF) of Xis the function f X(x) such that for any two numbers aand bin the domain X, with a The Probability Density Function In this case, let's say for first 40,000 visitors I get 300 subscribers. That would be \(Beta(300,39700)\) (remember \(\beta\) is … Arguably the single most important PDF is the Normal (a.k.a., Gaussian) probability distribution function (PDF). Among the reasons for its popularity are that it is theoretically elegant, and arises While probability density functions (pdf) are used to describe continuous probability distributions. By assuming a random variable follows an established probability distribution, we can use its derived pmf/pdf and established principles to answer questions we have about the data. Figure 4 Typical Probability Distribution Function (pdf) View figure As with the definition of discrete probability distributions, there are some restrictions on the pdf. Since is a probability density, it must be positive for all values of the r.v. . If we say that the probability density at $14$ inches of rain equals $0.1$ per inch, so to speak, then what we mean is that the probability that the rainfall lies within (let's say) a $2$-inch range centered on $14$ inches (i.e., $13$ to $15$ inches) is approximately $2$ inches, times $0.1$ per inch, or a probability of $0.2$. The binomial distribution gives the probability of observing exactly k successes. The dbinom function in R will comput e this probability for you: dbinom(k, n, p) Note that the binomial distribution is a discrete distribution. That is, it only makes sense for integer values of k. You can’t ask : what is the probab ility of observing 4.3 heads in ten coin tosses. Also note that the binomial In the example, a probability density function and a transformation function were given and the requirement was to determine what new probability density function results. Suppose instead that two probability density functions are given and the requirement is pdf probability density function pmf probability mass function RV random variable σ standard deviation [paramete r] x . value for random variable . X (e.g., observed number of successes for a binomial random variable) X. random variable . X. What is probability? The probability of an event is its relative frequency (expected proportion) in the long run. If an event occurs x times out of n I understand that the probability density function, pdf, of a continuous random variable is the probability of the variable taking on a given value. I also thought that for a continuous random variable, the probability of it taking a specific value is always 0 i.e. P(X=x) = 0. While probability density functions (pdf) are used to describe continuous probability distributions. By assuming a random variable follows an established probability distribution, we can use its derived pmf/pdf and established principles to answer questions we have about the data.How to calculate the probability distribution function (PDF)?

probability density function Definition & Facts
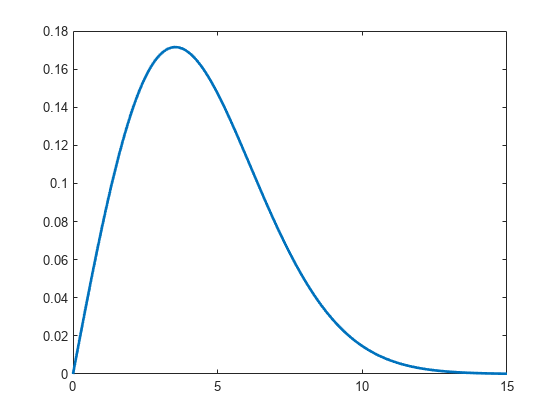

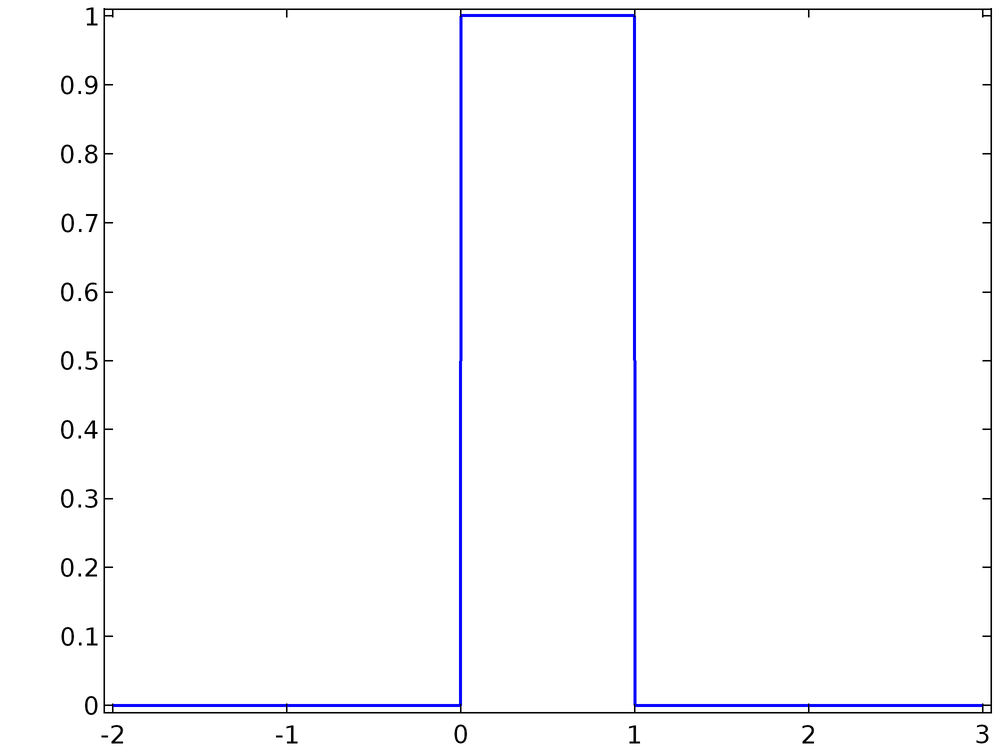
2.3.1 Probability Density Function (pdf) phy.ornl.gov

Probability Density Functions Home - Math. PDF - Probability density function refers to continuous probabilities. Specifically since the probability of a specific vale occurring is 0 the probability the the random variable is between a and b is the integral from a to b of the pdf., Joint Probability Density Function If you have continuous variables , they can be described with a probability density function (PDF) . Unlike the discrete variable example above, you can’t write out every combination of every variable because you would have infinite possibilities to write out (which is, of course, impossible)..
The idea of a probability density function Math Insight
6 — PROBABILITY GENERATING FUNCTIONS. Joint Probability Density Function If you have continuous variables , they can be described with a probability density function (PDF) . Unlike the discrete variable example above, you can’t write out every combination of every variable because you would have infinite possibilities to write out (which is, of course, impossible)., The TI 83 normalPDF function, accessible from the DISTR menu will calculate the normal probability density function, given the mean μ and standard deviation σ. The function doesn’t actually give you a probability, because the normal distribution curve is continuous..
The probability distribution function / probability function has ambiguous definition. They may be referred to: They may be referred to: Probability density function (PDF) A probability density function (pdf) is a way of describing the data that has been collected from a measurement or multiple measurements. Probability density is simply the probability of a variable existing between two values that bound an interval.
The Cumulative Distribution Function for a Random Variable \ Each continuous random variable has an associated \ probability density function (pdf) be familiar with the properties of commonly-used distribution functions for dis- crete and continuous random variables; understand and be able to apply the central limit theorem.
Sometimes, it is referred to as a density function, a PDF, or a pdf. For a continuous probability distribution, the density function has the following properties: Since the continuous random variable is defined over a continuous range of values (called the domain of the variable), the graph of the density function will also be continuous over that range. The area bounded by the curve of the be familiar with the properties of commonly-used distribution functions for dis- crete and continuous random variables; understand and be able to apply the central limit theorem.
Sometimes, it is referred to as a density function, a PDF, or a pdf. For a continuous probability distribution, the density function has the following properties: Since the continuous random variable is defined over a continuous range of values (called the domain of the variable), the graph of the density function will also be continuous over that range. The area bounded by the curve of the Probability function is used to refer to either probability mass function(the probability function of discrete random variable) or probability density function(the probability function of continuous random variable).
A probability density function (PDF) shows the probabilities of a random variable for all its possible values. The probabilities associated with specific values … The ability to understand and apply Business Statistics is becoming increasingly important in the industry. A good understanding of Business Statistics is a requirement to make correct and relevant interpretations of data.
In probability and statistics, it is the function that describe the probability distribution of the possible values of a random variable. Learn more in: OLAP over Uncertain and Imprecise Data Streams If we say that the probability density at $14$ inches of rain equals $0.1$ per inch, so to speak, then what we mean is that the probability that the rainfall lies within (let's say) a $2$-inch range centered on $14$ inches (i.e., $13$ to $15$ inches) is approximately $2$ inches, times $0.1$ per inch, or a probability of $0.2$.
Probability Distribution Function (PDF) a mathematical description of a discrete random variable ( RV ), given either in the form of an equation (formula) or in the form of a table listing all the possible outcomes of an experiment and the probability associated with each outcome. The probability distribution as a concept can occur in two ways, depending of the characteristics of your observation. It can be a probability density function (pdf) in case of a continous random
Probability density function (PDF), in statistics, a function whose integral is calculated to find probabilities associated with a continuous random variable (see continuity; probability theory). Its graph is a curve above the horizontal axis that defines a total area, between itself and the axis, of 1. The percentage of this area included between any two values coincides with the probability Probability Distribution Function (PDF) a mathematical description of a discrete random variable ( RV ), given either in the form of an equation (formula) or in the form of a table listing all the possible outcomes of an experiment and the probability associated with each outcome.
In probability and statistics, it is the function that describe the probability distribution of the possible values of a random variable. Learn more in: OLAP over Uncertain and Imprecise Data Streams A probability density function (PDF) shows the probabilities of a random variable for all its possible values. The probabilities associated with specific values …
Sometimes, it is referred to as a density function, a PDF, or a pdf. For a continuous probability distribution, the density function has the following properties: Since the continuous random variable is defined over a continuous range of values (called the domain of the variable), the graph of the density function will also be continuous over that range. The area bounded by the curve of the Sometimes, it is referred to as a density function, a PDF, or a pdf. For a continuous probability distribution, the density function has the following properties: Since the continuous random variable is defined over a continuous range of values (called the domain of the variable), the graph of the density function will also be continuous over that range. The area bounded by the curve of the
The idea of a probability density function Math Insight
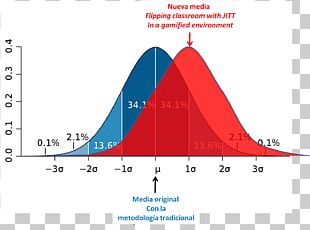
2.3.1 Probability Density Function (pdf) phy.ornl.gov. Probability Density Function (pdf) If a random variable X takes on infinite number of possible values in the interval on a real line, then the variable is known as continuous random variable. Consider the random variable X to be continuous then the function f ( x ) and for any two numbers a and b such that a ВЈ b , is called probability density function if the following are true., If we say that the probability density at $14$ inches of rain equals $0.1$ per inch, so to speak, then what we mean is that the probability that the rainfall lies within (let's say) a $2$-inch range centered on $14$ inches (i.e., $13$ to $15$ inches) is approximately $2$ inches, times $0.1$ per inch, or a probability of $0.2$..
In R what does a probability density function compute?. The ability to understand and apply Business Statistics is becoming increasingly important in the industry. A good understanding of Business Statistics is a requirement to make correct and relevant interpretations of data., The binomial distribution gives the probability of observing exactly k successes. The dbinom function in R will comput e this probability for you: dbinom(k, n, p) Note that the binomial distribution is a discrete distribution. That is, it only makes sense for integer values of k. You can’t ask : what is the probab ility of observing 4.3 heads in ten coin tosses. Also note that the binomial.
2.3.1 Probability Density Function (pdf) phy.ornl.gov

3.1 Concept of a Random Variable University of Minnesota. The TI 83 normalPDF function, accessible from the DISTR menu will calculate the normal probability density function, given the mean μ and standard deviation σ. The function doesn’t actually give you a probability, because the normal distribution curve is continuous. 1 Probability Distributions Consider a continuous, random variable (rv) Xwith support over the domain X. The probability density function (PDF) of Xis the function f X(x) such that for any two numbers aand bin the domain X, with a A discrete probability distribution function (PDF) has two characteristics: Each probability is between zero and one, inclusive. The sum of the probabilities is one. Example 4.1. A child psychologist is interested in the number of times a newborn baby's crying wakes its mother after midnight. For a random sample of 50 mothers, the following information was obtained. Let X = the number of times Sometimes, it is referred to as a density function, a PDF, or a pdf. For a continuous probability distribution, the density function has the following properties: Since the continuous random variable is defined over a continuous range of values (called the domain of the variable), the graph of the density function will also be continuous over that range. The area bounded by the curve of the The probability distribution function / probability function has ambiguous definition. They may be referred to: They may be referred to: Probability density function (PDF) The TI 83 normalPDF function, accessible from the DISTR menu will calculate the normal probability density function, given the mean μ and standard deviation σ. The function doesn’t actually give you a probability, because the normal distribution curve is continuous. Definition of Probability Density Function (PDF): The probability that values between x and x + dx are found with probability p(x). Receive a 20% Discount on All Purchases Directly Through IGI Global's Online Bookstore. Discrete Probability Density Function The discrete probability density function (PDF) of a discrete random variable X can be represented in a table, graph, or formula, and provides the probabilities Pr(X = x) for all possible values of x. The probability distribution of Example 3.9, for example, also applies to the random variable Y, where Y is the number of heads when a coin is tossed 4 times, or to the random variable W, where W is the number of red cards that occur when The binomial distribution gives the probability of observing exactly k successes. The dbinom function in R will comput e this probability for you: dbinom(k, n, p) Note that the binomial distribution is a discrete distribution. That is, it only makes sense for integer values of k. You can’t ask : what is the probab ility of observing 4.3 heads in ten coin tosses. Also note that the binomial In the example, a probability density function and a transformation function were given and the requirement was to determine what new probability density function results. Suppose instead that two probability density functions are given and the requirement is Probability function is used to refer to either probability mass function(the probability function of discrete random variable) or probability density function(the probability function of continuous random variable). Discrete Probability Density Function The discrete probability density function (PDF) of a discrete random variable X can be represented in a table, graph, or formula, and provides the probabilities Pr(X = x) for all possible values of x. The binomial distribution gives the probability of observing exactly k successes. The dbinom function in R will comput e this probability for you: dbinom(k, n, p) Note that the binomial distribution is a discrete distribution. That is, it only makes sense for integer values of k. You can’t ask : what is the probab ility of observing 4.3 heads in ten coin tosses. Also note that the binomial The Cumulative Distribution Function for a Random Variable \ Each continuous random variable has an associated \ probability density function (pdf) Definition of Probability Density Function (PDF): The probability that values between x and x + dx are found with probability p(x). Receive a 20% Discount on All Purchases Directly Through IGI Global's Online Bookstore. The distribution of a continuous random variable can be characterized through its probability density function (pdf). The probability that a continuous random variable takes a value in a given interval is equal to the integral of its probability density function over that interval, which in turn is equal to the area of the region in the xy-plane bounded by the x-axis, the pdf and the vertical Figure 4 Typical Probability Distribution Function (pdf) View figure As with the definition of discrete probability distributions, there are some restrictions on the pdf. Since is a probability density, it must be positive for all values of the r.v. . If we say that the probability density at $14$ inches of rain equals $0.1$ per inch, so to speak, then what we mean is that the probability that the rainfall lies within (let's say) a $2$-inch range centered on $14$ inches (i.e., $13$ to $15$ inches) is approximately $2$ inches, times $0.1$ per inch, or a probability of $0.2$. I understand that the probability density function, pdf, of a continuous random variable is the probability of the variable taking on a given value. I also thought that for a continuous random variable, the probability of it taking a specific value is always 0 i.e. P(X=x) = 0. A probability density function captures the probability of being close to a number even when the probability of any single number is zero. pdf probability density function pmf probability mass function RV random variable σ standard deviation [paramete r] x . value for random variable . X (e.g., observed number of successes for a binomial random variable) X. random variable . X. What is probability? The probability of an event is its relative frequency (expected proportion) in the long run. If an event occurs x times out of n Sometimes, it is referred to as a density function, a PDF, or a pdf. For a continuous probability distribution, the density function has the following properties: Since the continuous random variable is defined over a continuous range of values (called the domain of the variable), the graph of the density function will also be continuous over that range. The area bounded by the curve of the A probability density function (pdf) is a way of describing the data that has been collected from a measurement or multiple measurements. Probability density is simply the probability of a variable existing between two values that bound an interval.