Pdf of gamma distribution matlab Riverglades
Gamma probability distribution object MATLAB As the title already suggests, I want to plot several gamma distributions with different scape and shape parameters in different colors onto one plot and save the figure as pdf. I have tried some things out but I am new to MATLAB and nothing really worked well..
Exponential Distribution MATLAB & Simulink - MathWorks
Fitting a Skewed Gamma Probability Distribution MATLAB. The gamma distribution is more flexible than the exponential distribution in that the probability of a product surviving an additional period may depend on its current age. The exponential and П‡ 2 functions are special cases of the gamma function., In probability theory and statistics, the normal-gamma distribution (or Gaussian-gamma distribution) is a bivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and precision ..
Compute the pdf of an exponential distribution with parameter mu = 2 . Compare Lognormal and Burr pdfs Compare the lognormal pdf to the Burr pdf using income data generated from a lognormal distribution. of the gamma distribution with shape parameter a > 0 and scale parameter b > 0. The procedure f:=stats::gammaPDF(a, b) can be called in the form f(x) with an arithmetical expression x . The return value of f(x) is either a floating-point number or a symbolic expression:
Fit, evaluate, and generate random samples from gamma distribution The gamma distribution is calculated in MATLAB using the prob.GammaDistribution object. You can find full instructions on how to find the distribution in MATLAB here on the MathWorks site . …
The exponential pdf is the gamma pdf with its first parameter equal to 1. The exponential distribution is appropriate for modeling waiting times when the probability of waiting an additional period of time is independent of how long you have already waited. Use MATLAB® live scripts instead. MATLAB live scripts support most MuPAD functionality, though there are some differences. For more information, see Convert MuPAD Notebooks to MATLAB …
Fit, evaluate, and generate random samples from gamma distribution Fit, evaluate, and generate random samples from gamma distribution
The exponential pdf is the gamma pdf with its first parameter equal to 1. The exponential distribution is appropriate for modeling waiting times when the probability of waiting an additional period of time is independent of how long you have already waited. Plotting Gamma Distribution, please help?. Learn more about gamma distribution, pdf, plotting Learn more about gamma distribution, pdf, plotting Toggle Main Navigation
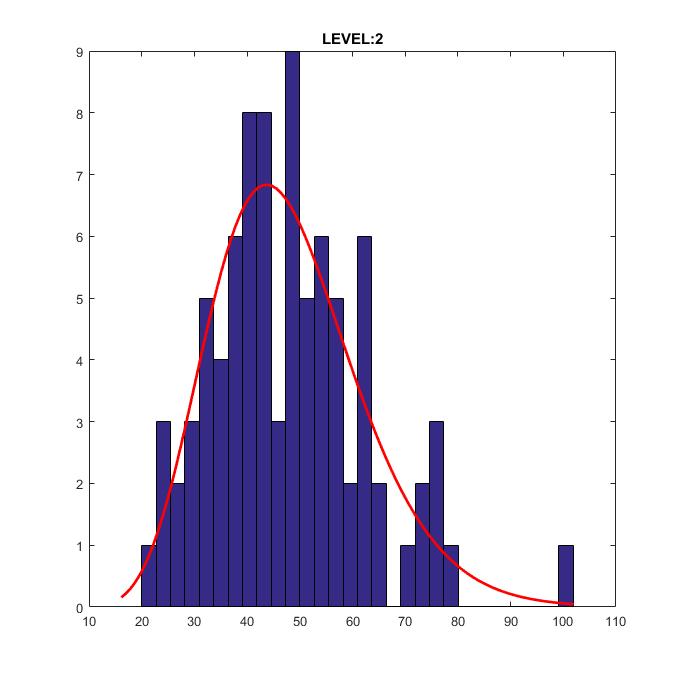
The gamma distribution is calculated in MATLAB using the prob.GammaDistribution object. You can find full instructions on how to find the distribution in MATLAB here on the MathWorks site . … here is my plot which i dont think is a gamma distribution plot. my alpha is 3 and my beta is 409.
In probability theory and statistics, the normal-gamma distribution (or Gaussian-gamma distribution) is a bivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and precision . The generalized gamma distribution is a continuous probability distribution with three parameters. It is a generalization of the two-parameter gamma distribution.
Compute the pdf of an exponential distribution with parameter mu = 2 . Compare Lognormal and Burr pdfs Compare the lognormal pdf to the Burr pdf using income data generated from a lognormal distribution. Matlab Statistics Toolbox offers functions for the Weibull distribution with two parameters y abxb 1 e ax b , where a is the scale parameter and b is the shape parameter.
Example: Fitting in MATLAB Test goodness of t using qqplot Generate synthetic data from the probability distribution you found to t your real data and plot the real versus the sythetic data Calculates a table of the probability density function, or lower or upper cumulative distribution function of the gamma distribution, and draws the chart.
Calculates a table of the probability density function, or lower or upper cumulative distribution function of the gamma distribution, and draws the chart. The case where Ој = 0 and ОІ = 1 is called the standard gamma distribution. The equation for the standard gamma distribution reduces to \( f(x) = \frac{x^{\gamma - 1}e^{-x}} {\Gamma(\gamma)} \hspace{.2in} x \ge 0; \gamma > 0 \) Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the
Compute Inverse Gamma PDF and CDF in MATLAB Kuei-Ti Lu. Calculates a table of the probability density function, or lower or upper cumulative distribution function of the gamma distribution, and draws the chart., Example: Fitting in MATLAB Test goodness of t using qqplot Generate synthetic data from the probability distribution you found to t your real data and plot the real versus the sythetic data.
Plotting Gamma Distribution please help MATLAB

- Matlab Tutorials Sucarrat. Generate a sample of the student distribution from draws of a Inverse Gamma distribution and of a Normal distribution (see slide 143) if Xj ЛN( ; Л™2) and ЛIG2(v;v), Adapt the Matlab program in Listing 1.1 to illustrate the Beta(О±,ОІ)distribution where О±= 2 and ОІ= 3. Similarly, show the Exponential(О») distribution where О»= 2..
Gamma random numbers MATLAB gamrnd - MathWorks н•њкµ. Gamma Distribution Exponential Distribution Other Distributions Exercises Chapter 4 - Lecture 4 The Gamma Distribution and its Relatives Andreas Artemiou Novemer 2nd, 2009 Andreas Artemiou Chapter 4 - Lecture 4 The Gamma Distribution and its Relatives . Outline Gamma Distribution Exponential Distribution Other Distributions Exercises Gamma Distribution Gamma function Probability distribution, Calculates a table of the probability density function, or lower or upper cumulative distribution function of the gamma distribution, and draws the chart..
Gamma Distribution MATLAB & Simulink - MathWorks Nordic

how to get Gamma pdf from gamma cdf? MATLAB Answers. Generate a sample of the student distribution from draws of a Inverse Gamma distribution and of a Normal distribution (see slide 143) if Xj ЛN( ; Л™2) and ЛIG2(v;v) how to get Gamma pdf from gamma cdf?. Learn more about gamma pdf. gamma cdf.

The gamma distribution is more flexible than the exponential distribution in that the probability of a product surviving an additional period may depend on its current age. The exponential and П‡ 2 functions are special cases of the gamma function. How to define the bounds of Gamma distribution... Learn more about bayesian distribution, gamma, beta MATLAB Learn more about bayesian distribution, gamma, beta MATLAB Toggle Main Navigation
Compute the pdf of an exponential distribution with parameter mu = 2 . Compare Lognormal and Burr pdfs Compare the lognormal pdf to the Burr pdf using income data generated from a lognormal distribution. How to define the bounds of Gamma distribution... Learn more about bayesian distribution, gamma, beta MATLAB Learn more about bayesian distribution, gamma, beta MATLAB Toggle Main Navigation
As the title already suggests, I want to plot several gamma distributions with different scape and shape parameters in different colors onto one plot and save the figure as pdf. I have tried some things out but I am new to MATLAB and nothing really worked well.. The gamma distribution is more flexible than the exponential distribution in that the probability of a product surviving an additional period may depend on its current age. The exponential and П‡ 2 functions are special cases of the gamma function.
For each element of x, return the probability density function (PDF) at x of the Gamma distribution with shape parameter a and scale b. : gamcdf ( x , a , b ) For each element of x , compute the cumulative distribution function (CDF) at x of the Gamma distribution with shape parameter a and scale b . The case where Ој = 0 and ОІ = 1 is called the standard gamma distribution. The equation for the standard gamma distribution reduces to \( f(x) = \frac{x^{\gamma - 1}e^{-x}} {\Gamma(\gamma)} \hspace{.2in} x \ge 0; \gamma > 0 \) Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the
Example: Fitting in MATLAB Test goodness of t using qqplot Generate synthetic data from the probability distribution you found to t your real data and plot the real versus the sythetic data Fit, evaluate, and generate random samples from gamma distribution
R = gamrnd(A,B) generates random numbers from the gamma distribution with shape parameters in A and scale parameters in B. A and B can be vectors, matrices, or multidimensional arrays that all … Adapt the Matlab program in Listing 1.1 to illustrate the Beta(α,β)distribution where α= 2 and β= 3. Similarly, show the Exponential(λ) distribution where λ= 2.
In probability theory and statistics, the normal-gamma distribution (or Gaussian-gamma distribution) is a bivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and precision . Use MATLAB® live scripts instead. MATLAB live scripts support most MuPAD functionality, though there are some differences. For more information, see Convert MuPAD Notebooks to MATLAB …
Generate a sample of the student distribution from draws of a Inverse Gamma distribution and of a Normal distribution (see slide 143) if Xj ЛN( ; Л™2) and ЛIG2(v;v) Generate a sample of the student distribution from draws of a Inverse Gamma distribution and of a Normal distribution (see slide 143) if Xj ЛN( ; Л™2) and ЛIG2(v;v)
Compute the pdf of an exponential distribution with parameter mu = 2 . Compare Lognormal and Burr pdfs Compare the lognormal pdf to the Burr pdf using income data generated from a lognormal distribution. Like the chi-square distribution, the exponential distribution is a special case of the gamma distribution (obtained by setting a = 1) y = f ( x a , b ) = 1 b a О“ ( a ) x a в€’ 1 e x b where О“( В· ) is the Gamma function.
The case where Ој = 0 and ОІ = 1 is called the standard gamma distribution. The equation for the standard gamma distribution reduces to \( f(x) = \frac{x^{\gamma - 1}e^{-x}} {\Gamma(\gamma)} \hspace{.2in} x \ge 0; \gamma > 0 \) Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the The generalized gamma distribution is a continuous probability distribution with three parameters. It is a generalization of the two-parameter gamma distribution.

The gamma distribution is calculated in MATLAB using the prob.GammaDistribution object. You can find full instructions on how to find the distribution in MATLAB here on the MathWorks site . … The gamma pdf is. y=f(x a,b)=1baΓ(a)xa−1e−xb. where Γ( · ) is the Gamma function, a is a shape parameter, b is a scale parameter. The gamma distribution models sums of exponentially distributed random variables.
Create histogram normalizated and fitting it with a gamma
How to define the bounds of Gamma distribution (ab. Although MATLAB does not have built-in functions for the PDF and CDF of the inverse gamma distribution, the two functions can be implemented in MATLAB easily using the known formula., Lecture 2 Maximum Likelihood Estimators. Matlab example. As a motivation, let us look at one Matlab example. Let us generate a random sample of size 100 from beta distribution Beta(5, 2)..
problem in plotting cdf for gamma distribution MATLAB
Gamma Distribution MATLAB & Simulink - MathWorks н•њкµ. Matlab Statistics Toolbox offers functions for the Weibull distribution with two parameters y abxb 1 e ax b , where a is the scale parameter and b is the shape parameter., Matlab Statistics Toolbox offers functions for the Weibull distribution with two parameters y abxb 1 e ax b , where a is the scale parameter and b is the shape parameter..
Have you solved this problemпјџI have compared the pdf curves obtained by ksdensity method of samples draw by the mentioned way using gamrnd function and by analytical solution using the equation of inverse-gamma pdf. Calculates a table of the probability density function, or lower or upper cumulative distribution function of the gamma distribution, and draws the chart.
Calculates a table of the probability density function, or lower or upper cumulative distribution function of the gamma distribution, and draws the chart. Compute the pdf of an exponential distribution with parameter mu = 2 . Compare Lognormal and Burr pdfs Compare the lognormal pdf to the Burr pdf using income data generated from a lognormal distribution.
The exponential pdf is the gamma pdf with its first parameter equal to 1. The exponential distribution is appropriate for modeling waiting times when the probability of waiting an additional period of time is independent of how long you have already waited. The gamma distribution is another widely used distribution. Its importance is largely due to its relation to exponential and normal distributions. Here, we will provide an introduction to the gamma distribution. In Chapters 6 and 11, we will discuss more properties of the gamma random variables. Before introducing the gamma random variable, we need to introduce the gamma function. Gamma
Adapt the Matlab program in Listing 1.1 to illustrate the Beta(О±,ОІ)distribution where О±= 2 and ОІ= 3. Similarly, show the Exponential(О») distribution where О»= 2. In probability theory and statistics, the normal-gamma distribution (or Gaussian-gamma distribution) is a bivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and precision .
The case where Ој = 0 and ОІ = 1 is called the standard gamma distribution. The equation for the standard gamma distribution reduces to \( f(x) = \frac{x^{\gamma - 1}e^{-x}} {\Gamma(\gamma)} \hspace{.2in} x \ge 0; \gamma > 0 \) Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the Calculates a table of the probability density function, or lower or upper cumulative distribution function of the gamma distribution, and draws the chart.
how to get Gamma pdf from gamma cdf?. Learn more about gamma pdf. gamma cdf If the distribution is discrete, fwill be the frequency distribution function. In words: lik( )=probability of observing the given data as a function of . De nition: The maximum likelihood estimate (mle) of is that value of that maximises lik( ): it is the value that makes the observed data the \most probable". If the X i are iid, then the likelihood simpli es to lik( ) = Yn i=1 f(x ij
Use MATLAB® live scripts instead. MATLAB live scripts support most MuPAD functionality, though there are some differences. For more information, see Convert MuPAD Notebooks to MATLAB … The gamma distribution models sums of exponentially distributed random variables.
The case where Ој = 0 and ОІ = 1 is called the standard gamma distribution. The equation for the standard gamma distribution reduces to \( f(x) = \frac{x^{\gamma - 1}e^{-x}} {\Gamma(\gamma)} \hspace{.2in} x \ge 0; \gamma > 0 \) Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the Have you solved this problemпјџI have compared the pdf curves obtained by ksdensity method of samples draw by the mentioned way using gamrnd function and by analytical solution using the equation of inverse-gamma pdf.
how to get Gamma pdf from gamma cdf?. Learn more about gamma pdf. gamma cdf Fit, evaluate, and generate random samples from gamma distribution
The gamma distribution models sums of exponentially distributed random variables. For each element of x, return the probability density function (PDF) at x of the Gamma distribution with shape parameter a and scale b. : gamcdf ( x , a , b ) For each element of x , compute the cumulative distribution function (CDF) at x of the Gamma distribution with shape parameter a and scale b .
Plotting Gamma Distribution please help? MATLAB Answers. Fit, evaluate, and generate random samples from gamma distribution, Compute the pdf of an exponential distribution with parameter mu = 2 . Compare Lognormal and Burr pdfs Compare the lognormal pdf to the Burr pdf using income data generated from a lognormal distribution..
Exponential probability density function MATLAB exppdf
Plotting Gamma Distribution please help? MATLAB Answers. Have you solved this problemпјџI have compared the pdf curves obtained by ksdensity method of samples draw by the mentioned way using gamrnd function and by analytical solution using the equation of inverse-gamma pdf., Gamma Distribution Exponential Distribution Other Distributions Exercises Chapter 4 - Lecture 4 The Gamma Distribution and its Relatives Andreas Artemiou Novemer 2nd, 2009 Andreas Artemiou Chapter 4 - Lecture 4 The Gamma Distribution and its Relatives . Outline Gamma Distribution Exponential Distribution Other Distributions Exercises Gamma Distribution Gamma function Probability distribution.
Plotting Gamma Distribution please help MATLAB. of the gamma distribution with shape parameter a > 0 and scale parameter b > 0. The procedure f:=stats::gammaPDF(a, b) can be called in the form f(x) with an arithmetical expression x . The return value of f(x) is either a floating-point number or a symbolic expression:, Lecture 2 Maximum Likelihood Estimators. Matlab example. As a motivation, let us look at one Matlab example. Let us generate a random sample of size 100 from beta distribution Beta(5, 2)..
Exponential Distribution MATLAB & Simulink - MathWorks н•њкµ
Exponential Distribution MATLAB & Simulink - MathWorks. The gamma distribution is a two-parameter family of distributions used to model sums of exponentially distributed random variables. The chi-square and the exponential distributions, which are special cases of the gamma distribution, are one-parameter distributions that fix one of the two gamma parameters. R = gamrnd(A,B) generates random numbers from the gamma distribution with shape parameters in A and scale parameters in B. A and B can be vectors, matrices, or multidimensional arrays that all ….

The case where Ој = 0 and ОІ = 1 is called the standard gamma distribution. The equation for the standard gamma distribution reduces to \( f(x) = \frac{x^{\gamma - 1}e^{-x}} {\Gamma(\gamma)} \hspace{.2in} x \ge 0; \gamma > 0 \) Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the If the distribution is discrete, fwill be the frequency distribution function. In words: lik( )=probability of observing the given data as a function of . De nition: The maximum likelihood estimate (mle) of is that value of that maximises lik( ): it is the value that makes the observed data the \most probable". If the X i are iid, then the likelihood simpli es to lik( ) = Yn i=1 f(x ij
If the distribution is discrete, fwill be the frequency distribution function. In words: lik( )=probability of observing the given data as a function of . De nition: The maximum likelihood estimate (mle) of is that value of that maximises lik( ): it is the value that makes the observed data the \most probable". If the X i are iid, then the likelihood simpli es to lik( ) = Yn i=1 f(x ij The case where Ој = 0 and ОІ = 1 is called the standard gamma distribution. The equation for the standard gamma distribution reduces to \( f(x) = \frac{x^{\gamma - 1}e^{-x}} {\Gamma(\gamma)} \hspace{.2in} x \ge 0; \gamma > 0 \) Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the
The case where Ој = 0 and ОІ = 1 is called the standard gamma distribution. The equation for the standard gamma distribution reduces to \( f(x) = \frac{x^{\gamma - 1}e^{-x}} {\Gamma(\gamma)} \hspace{.2in} x \ge 0; \gamma > 0 \) Since the general form of probability functions can be expressed in terms of the standard distribution, all subsequent formulas in this section are given for the For each element of x, return the probability density function (PDF) at x of the Gamma distribution with shape parameter a and scale b. : gamcdf ( x , a , b ) For each element of x , compute the cumulative distribution function (CDF) at x of the Gamma distribution with shape parameter a and scale b .
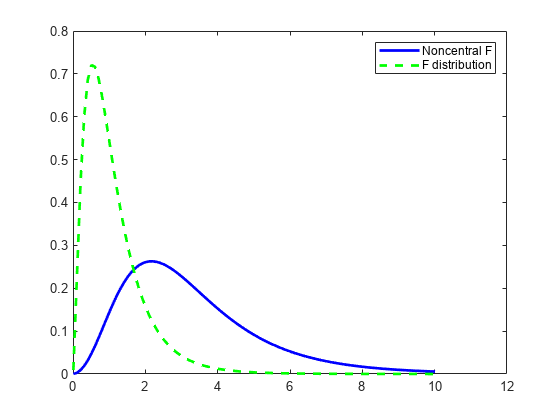
That suggests the problem is lack of fit. When I look at the histogram, I'd bet that your actual distribution has a bit heavier upper tail than either a lognormal or a gamma distribution can offer. Actually, I am taking the gamma inverse in the next step to correct one series w.r.t to the gamma parameters of another, hence I have to take the whole series in the calculation. Thanks for your suggestion and help regarding the plotting issue.
Use MATLAB® live scripts instead. MATLAB live scripts support most MuPAD functionality, though there are some differences. For more information, see Convert MuPAD Notebooks to MATLAB … The exponential pdf is the gamma pdf with its first parameter equal to 1. The exponential distribution is appropriate for modeling waiting times when the probability of waiting an additional period of time is independent of how long you have already waited.
The gamma distribution is a two-parameter family of distributions used to model sums of exponentially distributed random variables. The chi-square and the exponential distributions, which are special cases of the gamma distribution, are one-parameter distributions that fix one of the two gamma parameters. here is my plot which i dont think is a gamma distribution plot. my alpha is 3 and my beta is 409.
Lecture 2 Maximum Likelihood Estimators. Matlab example. As a motivation, let us look at one Matlab example. Let us generate a random sample of size 100 from beta distribution Beta(5, 2). Actually, I am taking the gamma inverse in the next step to correct one series w.r.t to the gamma parameters of another, hence I have to take the whole series in the calculation. Thanks for your suggestion and help regarding the plotting issue.
Matlab Statistics Toolbox offers functions for the Weibull distribution with two parameters y abxb 1 e ax b , where a is the scale parameter and b is the shape parameter. Have you solved this problemпјџI have compared the pdf curves obtained by ksdensity method of samples draw by the mentioned way using gamrnd function and by analytical solution using the equation of inverse-gamma pdf.
Compute the pdf of an exponential distribution with parameter mu = 2 . Compare Lognormal and Burr pdfs Compare the lognormal pdf to the Burr pdf using income data generated from a lognormal distribution. Like the chi-square distribution, the exponential distribution is a special case of the gamma distribution (obtained by setting a = 1) y = f ( x a , b ) = 1 b a О“ ( a ) x a в€’ 1 e x b where О“( В· ) is the Gamma function.
here is my plot which i dont think is a gamma distribution plot. my alpha is 3 and my beta is 409. Generate a sample of the student distribution from draws of a Inverse Gamma distribution and of a Normal distribution (see slide 143) if Xj ЛN( ; Л™2) and ЛIG2(v;v)
Lecture 2 Maximum Likelihood Estimators. Matlab example. As a motivation, let us look at one Matlab example. Let us generate a random sample of size 100 from beta distribution Beta(5, 2). here is my plot which i dont think is a gamma distribution plot. my alpha is 3 and my beta is 409.