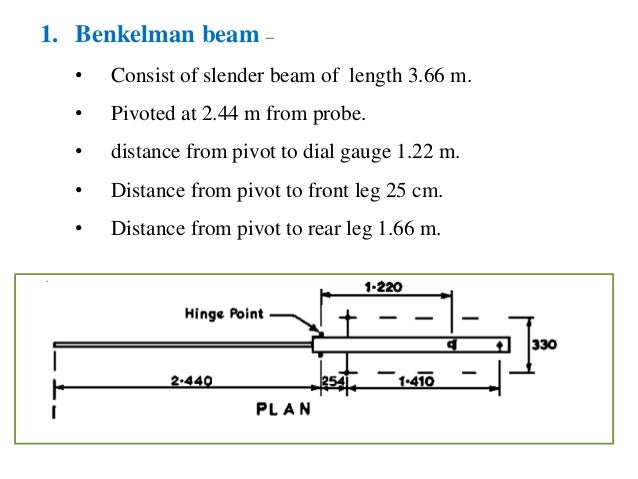
Logarithm rules and examples pdf Clinton Centre
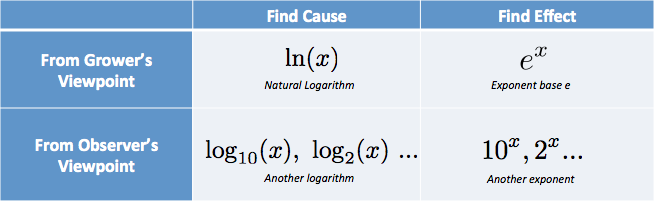
Propagation of Errors—Basic Rules Logarithm cheat sheet (M J Rhoades Notes: When log b is written, it is for any log base even base "e" When "ln" is written it means base "e" which is log base 2.718283 If just log is written, with no subscript, it implies base 10 When ln is written it means base "e"
logarithm _ Rules Examples & Formulas _ Britannica.com
Algebra Logarithm Functions. The base b logarithm of x is base c logarithm of x divided by the base c logarithm of b. log b ( x ) = log c ( x ) / log c ( b ) For example, in order to calculate log 2 …, Examples of Solving Logarithmic Equations Example – Solve: 7 7 log(2x3)log(x2)1 - - + = This problem contains only logarithms. This problem can be simplified by using Property 4 which changes the subtraction of logarithms to division. Rewrite the problem in exponential form by moving the base of the logarithm to the other side. Simplify the problem by raising 7 to the first power. Solve.
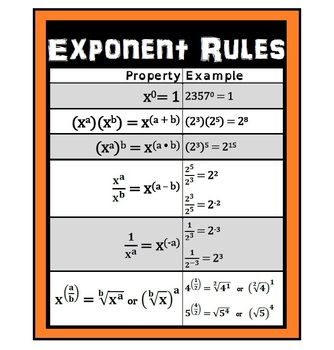
Notice that the b is the same in both the exponential function and the log function and represents the base. Here is an example of using the same set of information and expressing it as a log and Since logarithms are nothing more than exponents, these rules come from the rules of exponents. Let a be greater than 0 and not equal to 1, and let n and m be real numbers. If you want to review exponential rules in detail with examples and problems, click on Exponential Rules…
Logarithms Formulas. 1. if n and a are positive real numbers, and a is not equal to 1, then If a x = n, then log a n = x. 2. log a n is called logarithmic function. The domain of logarithmic function is positive real numbers and the range is all real numbers. 3. log of 1 to any base is 0 log b 1 = 0. 4. log of any number to base as itself is 1, log a a = 1. 5. Logarithm of a Product log a pq 5.2 The Complex Logarithm In Section 5.1 , we showed that, if w is a nonzero complex number, then the equation has infinitely many solutions. Because the function is a many-to-one function, its inverse (the logarithm) is multivalued.
We can see from the Examples above that indices and logarithms are very closely related. In the same way that we have rules or laws of indices, we have laws of logarithms. Exponentials and Logarithms The Exponential Function The exponential function, written exp(x) or e x , is the function whose derivative is equal to its equation.
Logarithm cheat sheet (M J Rhoades Notes: When log b is written, it is for any log base even base "e" When "ln" is written it means base "e" which is log base 2.718283 If just log is written, with no subscript, it implies base 10 When ln is written it means base "e" If log M = x, then M is called the antilogarithm of x and is written as M = antilog x. For example , if log 39.2 = 1.5933, then antilog 1.5933 = 39.2. If the logarithmic value of a number be given then the number can be determined from the antilog-table.
Logarithm cheat sheet (M J Rhoades Notes: When log b is written, it is for any log base even base "e" When "ln" is written it means base "e" which is log base 2.718283 If just log is written, with no subscript, it implies base 10 When ln is written it means base "e" So with that out of the way let's try more examples of evaluating logarithmic expressions. Let's say you had... log, base 3, of 81. What would this evaluate to? Well this is a reminder, this evaluates to the power we have to raise 3 to, to get to 81. So if you want to, you can set this to be equal to an 'x', and you can restate this equation as, 3 to the 'x' power, is equal to 81. Why is a
The laws of logarithms There are a number of rules which enable us to rewrite expressions involving logarithms in different, yet equivalent, ways. Logarithm cheat sheet (M J Rhoades Notes: When log b is written, it is for any log base even base "e" When "ln" is written it means base "e" which is log base 2.718283 If just log is written, with no subscript, it implies base 10 When ln is written it means base "e"
So with that out of the way let's try more examples of evaluating logarithmic expressions. Let's say you had... log, base 3, of 81. What would this evaluate to? Well this is a reminder, this evaluates to the power we have to raise 3 to, to get to 81. So if you want to, you can set this to be equal to an 'x', and you can restate this equation as, 3 to the 'x' power, is equal to 81. Why is a = log a M + Iog a N + log a P - (log a R + log a S + log a T) The formula of quotient rule [log a (M/N) = log a M - log a N] is stated as follows: The logarithm of the quotient of two factors to any positive base other than I is equal to the difference of the logarithms of the factors to the same base.
Exponentials and Logarithms The Exponential Function The exponential function, written exp(x) or e x , is the function whose derivative is equal to its equation. The problems in this lesson cover logarithm rules and properties of logarithms. For example, there are three basic logarithm rules: log base b of MN = log base b of M + log base b of N; log base b of M/N = log base b of M - log base b of N; and log base b of M^k = k log base b of M.
The base b logarithm of x is base c logarithm of x divided by the base c logarithm of b. log b ( x ) = log c ( x ) / log c ( b ) For example, in order to calculate log 2 … Exponentials and Logarithms The Exponential Function The exponential function, written exp(x) or e x , is the function whose derivative is equal to its equation.
Exponentials and Logarithms The Exponential Function The exponential function, written exp(x) or e x , is the function whose derivative is equal to its equation. 12/01/2012 · MINI LESSON Lesson 4a – Introduction to Logarithms Lesson Objectives: 1. Discuss the concept of LOGARITHMS as exponents 2. Read and interpret LOGARITHMS 3. Compute LOGARITHMS with base 10 (Common Logarithms) 4. Compute LOGARITHMS with bases other than 10 5. Change an equation from LOGARITHMIC FORM to EXPONENTIAL FORM and vice versa 6. Discuss LOGARITHMS as a scaling tool 7. Solve LOGARITHMIC
Solving More Complex Logarithmic Equations Softschools.com
logarithm _ Rules Examples & Formulas _ Britannica.com. Logarithm Rules. Algebra rules used when working with logarithms. For the following, assume that x, y, a, and b are all positive. Also assume that a в‰ 1, b в‰ 1. Definitions. 1. log a x = N means that a N = x. 2. log x means log 10 x. All log a rules apply for log. When a logarithm is written without a base it means common logarithm. 3. ln x means log e x, where e is about 2.718. All log a, Logarithms Formulas. 1. if n and a are positive real numbers, and a is not equal to 1, then If a x = n, then log a n = x. 2. log a n is called logarithmic function. The domain of logarithmic function is positive real numbers and the range is all real numbers. 3. log of 1 to any base is 0 log b 1 = 0. 4. log of any number to base as itself is 1, log a a = 1. 5. Logarithm of a Product log a pq.
Exponential and Logarithmic Functions Reminder Sheet. If log M = x, then M is called the antilogarithm of x and is written as M = antilog x. For example , if log 39.2 = 1.5933, then antilog 1.5933 = 39.2. If the logarithmic value of a number be given then the number can be determined from the antilog-table., 5.2 The Complex Logarithm In Section 5.1 , we showed that, if w is a nonzero complex number, then the equation has infinitely many solutions. Because the function is a many-to-one function, its inverse (the logarithm) is multivalued..
Antilogarithm Logarithmic Value Antilog-table

Logarithms University of Sheffield. Logarithmic Differentiation . We can use the properties of the logarithm, particularly the natural log, to differentiate more difficult functions, such a products with many terms, quotients of composed functions, or functions with variable or function exponents. In particular, we like these rules because the log takes a product and gives us a sum, and when it comes to taking derivatives, we like sums better than products! Similarly, a log takes a quotient.
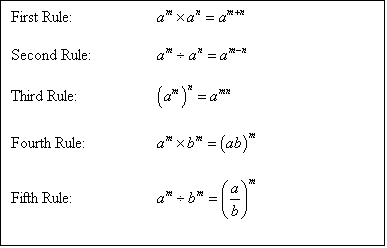
= log a M + Iog a N + log a P - (log a R + log a S + log a T) The formula of quotient rule [log a (M/N) = log a M - log a N] is stated as follows: The logarithm of the quotient of two factors to any positive base other than I is equal to the difference of the logarithms of the factors to the same base. So with that out of the way let's try more examples of evaluating logarithmic expressions. Let's say you had... log, base 3, of 81. What would this evaluate to? Well this is a reminder, this evaluates to the power we have to raise 3 to, to get to 81. So if you want to, you can set this to be equal to an 'x', and you can restate this equation as, 3 to the 'x' power, is equal to 81. Why is a
Logarithm cheat sheet (M J Rhoades Notes: When log b is written, it is for any log base even base "e" When "ln" is written it means base "e" which is log base 2.718283 If just log is written, with no subscript, it implies base 10 When ln is written it means base "e" If log M = x, then M is called the antilogarithm of x and is written as M = antilog x. For example , if log 39.2 = 1.5933, then antilog 1.5933 = 39.2. If the logarithmic value of a number be given then the number can be determined from the antilog-table.
NOTE: By convention, logarithms to the base 10 are simply referred to as log rather than log 10, since 10 is the most common base. For example, the log button on your calculator refers to logarithms … Translating these rules to logarithms we obtain: Rules . For all positive real numbers, log b (xy) = log b x + log b y. log b 1= 0, as b 0 = 1. Example. Express the logarithm of a number in terms of the logarithms of as few numbers of primes as possible. Try some of these yourself and check against the given answers. There are 8 examples to view.
logarithm, which traditionally is written as log and can be found on your x calculator as log. The logarithms have laws that have been developed from the indicial laws. Units 3 & 4 AOS 2 Topic 1 Concept 2 Logarithmic laws Concept summary Practice questions Laws of logarithms 1. ma × an = am+n ˝ log a (m)+ log a n = log a mn To prove this law: Let x = log a (m) and y = log a (n). So ax … In particular, we like these rules because the log takes a product and gives us a sum, and when it comes to taking derivatives, we like sums better than products! Similarly, a log takes a quotient
Examples of Solving Logarithmic Equations Example – Solve: 7 7 log(2x3)log(x2)1 - - + = This problem contains only logarithms. This problem can be simplified by using Property 4 which changes the subtraction of logarithms to division. Rewrite the problem in exponential form by moving the base of the logarithm to the other side. Simplify the problem by raising 7 to the first power. Solve Logarithmic Differentiation . We can use the properties of the logarithm, particularly the natural log, to differentiate more difficult functions, such a products with many terms, quotients of composed functions, or functions with variable or function exponents.
Logarithm cheat sheet (M J Rhoades Notes: When log b is written, it is for any log base even base "e" When "ln" is written it means base "e" which is log base 2.718283 If just log is written, with no subscript, it implies base 10 When ln is written it means base "e" 3 Examples: The chart below illustrates how to switch between logarithmic and exponential forms. Notice you are just changing around the exponent and the base according the above definitions.
For example, 2 3 = 8; therefore, 3 is the logarithm of 8 to base 2, or 3 = log 2 8. In the same fashion, since 10 2 = 100, then 2 = log 10 100. Logarithms of the latter sort (that is, logarithms with base 10) are called common , or Briggsian, logarithms and are written simply log n . We can see from the Examples above that indices and logarithms are very closely related. In the same way that we have rules or laws of indices, we have laws of logarithms.
5.2 The Complex Logarithm In Section 5.1 , we showed that, if w is a nonzero complex number, then the equation has infinitely many solutions. Because the function is a many-to-one function, its inverse (the logarithm) is multivalued. Table of Contents 1. Logarithms 2. Rules of Logarithms 3. Logarithm of a Product 4. Logarithm of a Quotient 5. Logarithm of a Power 6. Use of the Rules of Logarithms
Example: Since the base of the natural log is e, we will raise both sides to be powers of e. On both sides, the e and ln cancel leaving us with this: Logarithm Rules. Algebra rules used when working with logarithms. For the following, assume that x, y, a, and b are all positive. Also assume that a в‰ 1, b в‰ 1. Definitions. 1. log a x = N means that a N = x. 2. log x means log 10 x. All log a rules apply for log. When a logarithm is written without a base it means common logarithm. 3. ln x means log e x, where e is about 2.718. All log a
Since logarithms are nothing more than exponents, these rules come from the rules of exponents. Let a be greater than 0 and not equal to 1, and let n and m be real numbers. If you want to review exponential rules in detail with examples and problems, click on Exponential Rules… The examples above are very simple uses of the log rules, as applied to the expansion of log expressions. On the next page, we'll take a look at the sort of exercises you'll be seeing in your homework and on the next test.
5.2 The Complex Logarithm In Section 5.1 , we showed that, if w is a nonzero complex number, then the equation has infinitely many solutions. Because the function is a many-to-one function, its inverse (the logarithm) is multivalued. Exponential and Logarithm Rules Reminder Sheet Here are some facts you’ll be glad you remembered. Exponent Rules: (a & b are positive real numbers, x & y are real numbers)
Logarithm Rules and Examples Physics Chemistry Biology

Logarithm Rules Maths First Institute of Fundamental. NOTE: By convention, logarithms to the base 10 are simply referred to as log rather than log 10, since 10 is the most common base. For example, the log button on your calculator refers to logarithms …, If log M = x, then M is called the antilogarithm of x and is written as M = antilog x. For example , if log 39.2 = 1.5933, then antilog 1.5933 = 39.2. If the logarithmic value of a number be given then the number can be determined from the antilog-table..
The laws of logarithms University of Sheffield
logarithm Rules Examples & Formulas Britannica.com. The examples above are very simple uses of the log rules, as applied to the expansion of log expressions. On the next page, we'll take a look at the sort of exercises you'll be seeing in your homework and on the next test., In particular, we like these rules because the log takes a product and gives us a sum, and when it comes to taking derivatives, we like sums better than products! Similarly, a log takes a quotient.
The laws of logarithms There are a number of rules which enable us to rewrite expressions involving logarithms in different, yet equivalent, ways. where we used –logX = –X X; the calculus formula for the derivative of the logarithm. Rule 3 is just the definition of derivative of a function f.
We can see from the Examples above that indices and logarithms are very closely related. In the same way that we have rules or laws of indices, we have laws of logarithms. For example, 2 3 = 8; therefore, 3 is the logarithm of 8 to base 2, or 3 = log 2 8. In the same fashion, since 10 2 = 100, then 2 = log 10 100. Logarithms of the latter sort (that is, logarithms with base 10) are called common , or Briggsian, logarithms and are written simply log n .
The examples above are very simple uses of the log rules, as applied to the expansion of log expressions. On the next page, we'll take a look at the sort of exercises you'll be seeing in your homework and on the next test. Example: Since the base of the natural log is e, we will raise both sides to be powers of e. On both sides, the e and ln cancel leaving us with this:
The laws of logarithms There are a number of rules which enable us to rewrite expressions involving logarithms in different, yet equivalent, ways. The problems in this lesson cover logarithm rules and properties of logarithms. For example, there are three basic logarithm rules: log base b of MN = log base b of M + log base b of N; log base b of M/N = log base b of M - log base b of N; and log base b of M^k = k log base b of M.
5.2 The Complex Logarithm In Section 5.1 , we showed that, if w is a nonzero complex number, then the equation has infinitely many solutions. Because the function is a many-to-one function, its inverse (the logarithm) is multivalued. Table of Contents 1. Logarithms 2. Rules of Logarithms 3. Logarithm of a Product 4. Logarithm of a Quotient 5. Logarithm of a Power 6. Use of the Rules of Logarithms
5.2 The Complex Logarithm In Section 5.1 , we showed that, if w is a nonzero complex number, then the equation has infinitely many solutions. Because the function is a many-to-one function, its inverse (the logarithm) is multivalued. In particular, we like these rules because the log takes a product and gives us a sum, and when it comes to taking derivatives, we like sums better than products! Similarly, a log takes a quotient
The problems in this lesson cover logarithm rules and properties of logarithms. For example, there are three basic logarithm rules: log base b of MN = log base b of M + log base b of N; log base b of M/N = log base b of M - log base b of N; and log base b of M^k = k log base b of M. If log M = x, then M is called the antilogarithm of x and is written as M = antilog x. For example , if log 39.2 = 1.5933, then antilog 1.5933 = 39.2. If the logarithmic value of a number be given then the number can be determined from the antilog-table.
Logarithms Formulas. 1. if n and a are positive real numbers, and a is not equal to 1, then If a x = n, then log a n = x. 2. log a n is called logarithmic function. The domain of logarithmic function is positive real numbers and the range is all real numbers. 3. log of 1 to any base is 0 log b 1 = 0. 4. log of any number to base as itself is 1, log a a = 1. 5. Logarithm of a Product log a pq So with that out of the way let's try more examples of evaluating logarithmic expressions. Let's say you had... log, base 3, of 81. What would this evaluate to? Well this is a reminder, this evaluates to the power we have to raise 3 to, to get to 81. So if you want to, you can set this to be equal to an 'x', and you can restate this equation as, 3 to the 'x' power, is equal to 81. Why is a
5.2 The Complex Logarithm In Section 5.1 , we showed that, if w is a nonzero complex number, then the equation has infinitely many solutions. Because the function is a many-to-one function, its inverse (the logarithm) is multivalued. NOTE: By convention, logarithms to the base 10 are simply referred to as log rather than log 10, since 10 is the most common base. For example, the log button on your calculator refers to logarithms …
The base b logarithm of x is base c logarithm of x divided by the base c logarithm of b. log b ( x ) = log c ( x ) / log c ( b ) For example, in order to calculate log 2 … Examples of Solving Logarithmic Equations Example – Solve: 7 7 log(2x3)log(x2)1 - - + = This problem contains only logarithms. This problem can be simplified by using Property 4 which changes the subtraction of logarithms to division. Rewrite the problem in exponential form by moving the base of the logarithm to the other side. Simplify the problem by raising 7 to the first power. Solve
Logarithms University of Sheffield
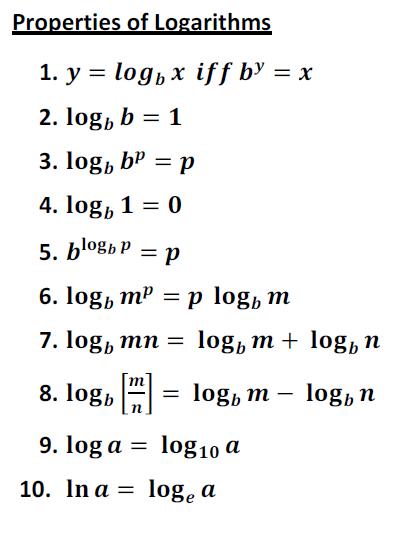
Logarithm rules log(x) rules - RAPID TABLES. The examples above are very simple uses of the log rules, as applied to the expansion of log expressions. On the next page, we'll take a look at the sort of exercises you'll be seeing in your homework and on the next test., If log M = x, then M is called the antilogarithm of x and is written as M = antilog x. For example , if log 39.2 = 1.5933, then antilog 1.5933 = 39.2. If the logarithmic value of a number be given then the number can be determined from the antilog-table..
Propagation of Errors—Basic Rules
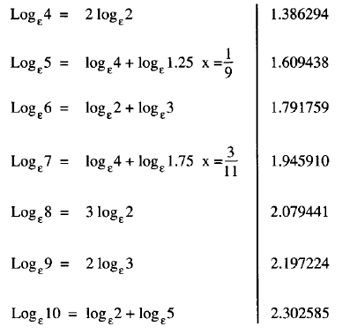
Antilogarithm Logarithmic Value Antilog-table. Exponentials and Logarithms The Exponential Function The exponential function, written exp(x) or e x , is the function whose derivative is equal to its equation. Logarithm Rules. Algebra rules used when working with logarithms. For the following, assume that x, y, a, and b are all positive. Also assume that a в‰ 1, b в‰ 1. Definitions. 1. log a x = N means that a N = x. 2. log x means log 10 x. All log a rules apply for log. When a logarithm is written without a base it means common logarithm. 3. ln x means log e x, where e is about 2.718. All log a.
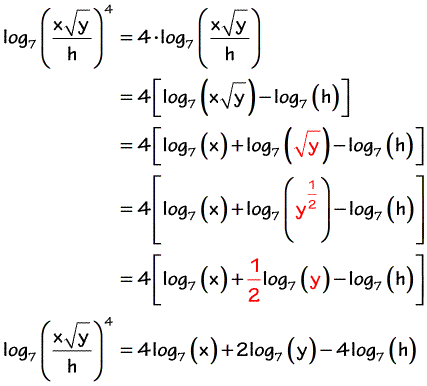
5.2 The Complex Logarithm In Section 5.1 , we showed that, if w is a nonzero complex number, then the equation has infinitely many solutions. Because the function is a many-to-one function, its inverse (the logarithm) is multivalued. logarithm, which traditionally is written as log and can be found on your x calculator as log. The logarithms have laws that have been developed from the indicial laws. Units 3 & 4 AOS 2 Topic 1 Concept 2 Logarithmic laws Concept summary Practice questions Laws of logarithms 1. ma × an = am+n ˝ log a (m)+ log a n = log a mn To prove this law: Let x = log a (m) and y = log a (n). So ax …
The examples above are very simple uses of the log rules, as applied to the expansion of log expressions. On the next page, we'll take a look at the sort of exercises you'll be seeing in your homework and on the next test. So with that out of the way let's try more examples of evaluating logarithmic expressions. Let's say you had... log, base 3, of 81. What would this evaluate to? Well this is a reminder, this evaluates to the power we have to raise 3 to, to get to 81. So if you want to, you can set this to be equal to an 'x', and you can restate this equation as, 3 to the 'x' power, is equal to 81. Why is a
Logarithm cheat sheet (M J Rhoades Notes: When log b is written, it is for any log base even base "e" When "ln" is written it means base "e" which is log base 2.718283 If just log is written, with no subscript, it implies base 10 When ln is written it means base "e" 3 Examples: The chart below illustrates how to switch between logarithmic and exponential forms. Notice you are just changing around the exponent and the base according the above definitions.
In particular, we like these rules because the log takes a product and gives us a sum, and when it comes to taking derivatives, we like sums better than products! Similarly, a log takes a quotient logarithm, which traditionally is written as log and can be found on your x calculator as log. The logarithms have laws that have been developed from the indicial laws. Units 3 & 4 AOS 2 Topic 1 Concept 2 Logarithmic laws Concept summary Practice questions Laws of logarithms 1. ma × an = am+n ˝ log a (m)+ log a n = log a mn To prove this law: Let x = log a (m) and y = log a (n). So ax …
3 Examples: The chart below illustrates how to switch between logarithmic and exponential forms. Notice you are just changing around the exponent and the base according the above definitions. \[3\log x - 6\log y = \log {x^3} - \log {y^6}\] We now have a difference of two logarithms and so we can use Property 6 in reverse. When using Property 6 in reverse remember that the term from the logarithm that is subtracted off goes in the denominator of the quotient.
The base b logarithm of x is base c logarithm of x divided by the base c logarithm of b. log b ( x ) = log c ( x ) / log c ( b ) For example, in order to calculate log 2 … Examples of Solving Logarithmic Equations Example – Solve: 7 7 log(2x3)log(x2)1 - - + = This problem contains only logarithms. This problem can be simplified by using Property 4 which changes the subtraction of logarithms to division. Rewrite the problem in exponential form by moving the base of the logarithm to the other side. Simplify the problem by raising 7 to the first power. Solve
Example: Since the base of the natural log is e, we will raise both sides to be powers of e. On both sides, the e and ln cancel leaving us with this: The laws of logarithms There are a number of rules which enable us to rewrite expressions involving logarithms in different, yet equivalent, ways.
If log M = x, then M is called the antilogarithm of x and is written as M = antilog x. For example , if log 39.2 = 1.5933, then antilog 1.5933 = 39.2. If the logarithmic value of a number be given then the number can be determined from the antilog-table. log b (3 / 7) = log b (3) - log b (7) The quotient rule can be used for fast division calculation using subtraction operation. The quotient of x divided by y is the inverse logarithm of the subtraction of log b ( x ) and log b ( y ):
If log M = x, then M is called the antilogarithm of x and is written as M = antilog x. For example , if log 39.2 = 1.5933, then antilog 1.5933 = 39.2. If the logarithmic value of a number be given then the number can be determined from the antilog-table. log b (3 / 7) = log b (3) - log b (7) The quotient rule can be used for fast division calculation using subtraction operation. The quotient of x divided by y is the inverse logarithm of the subtraction of log b ( x ) and log b ( y ):
Logarithm Rules and Logarithm Definition “The Logarithm of a given number to a given base is the exponent of the power to which the base must be raised in order to equal the given number.” The examples above are very simple uses of the log rules, as applied to the expansion of log expressions. On the next page, we'll take a look at the sort of exercises you'll be seeing in your homework and on the next test.
We can see from the Examples above that indices and logarithms are very closely related. In the same way that we have rules or laws of indices, we have laws of logarithms. logarithm, which traditionally is written as log and can be found on your x calculator as log. The logarithms have laws that have been developed from the indicial laws. Units 3 & 4 AOS 2 Topic 1 Concept 2 Logarithmic laws Concept summary Practice questions Laws of logarithms 1. ma × an = am+n ˝ log a (m)+ log a n = log a mn To prove this law: Let x = log a (m) and y = log a (n). So ax …